primeiro módulo Introdução, ASN.1

Roteiro Segundo Módulo

C2-2  Os padrões PKCS#1 e  PKCS#8 para cifragem e assinatura
 

Detentora, até setembro de 2000, da patente do RSA, o primeiro algoritmo critpográfico assimétrico a resistir o critério de assimetria (controle do custo para se obter a chave privada a partir da chave pública com uma implementação sadia do algoritmo gerador do par de chaves),  a RSADSI publicou, no início dos anos 90, uma série de recomendações contendo especificações visando padronizar os formatos e operações criptográficas baseadas neste algoritmo.

Essa família de recomendações é conhecida pela sigla PKCS (Public Key Cryptographic Stantards) compreendendo os documentos PKCS #1, #3, #5, #7, #8, #9, #10 #11, #12, #13, #14 e #15 (repositório em ttp://www.rsasecurity.com/rsalabs/pkcs/). Devido a seu pioneirismo e simplicidade do algoritmo, tornaram-se padrão de fato em PKIs .  Iremos abordar os padrões PKCS #1, que trata das primitivas critpográficas, dos esquemas de cifragem e assinatura digital  e PKCS #8, que trata da sintaxe para armazenamento e uso de chaves privadas.

C2-2.1 PKCS#1: Primitivas e esquemas de cifragem e assinatura com o RSA

C2-2.1.1- Versão 2.1 do documento PKCS#1
 
A especificação PKCS#1 passou por várias revisões, sendo que a versão atual (v.2.1) foi publicada em 14 de junho de 2002, supostamente mantendo a compatibilidade com as especificações anteriores. a v.2.1 contém, entre outros acréscimos relativos à funcionalidade do algoritmo RSA, diferentes esquemas para particionamento da chave privada baseados no teorema do resto chinês (ali abreviado como CRT). O documento está assim dividido
 
• Seção 1 Introducão.
• Seção 2 Notação
• Seção 3 Define os tipos de chave pública e privada do algoritmo RSA.
• Seção 4 and 5 define várias primitivas, dentre conversores de formato (4) e operações matemáticas elementares envolvendo inteiros extendidos, para cifragem/decifragem, lavra/verificação de assinaturas (5).
• Seção 6, 7, and 8 descrevem esquemas para lavra e verificação de assinaturas, e para cifragem e decifragem de dados.
• Seção 9 define métodos de codificação para os esquemas de assinatura descritos na seção 8.


O conteúdo das seções 1 a 5 foram cobertos no curso C1 (pre-requisito para este curso), de forma que iremos nos ater, neste módulo, a uma síntese das seções 6 a 9.
 
 

C2-2.1.2 Notação (reproduzida de PKCS#1 v2.1)
 
 

símbolo	significado
c	inteiro entre 0 e n – 1 que representa internamente o criptograma
C	criptograma codificado como cadeia de octetos
d	inteiro positivo, expoente da chave privada RSA
di	inteiro positivo satisfazendo e · di = 1 (mod (ri – 1)), i = 3,..., u, expoente do sistema de equações do resto chinês (CRT) correspondente ao fator primo ri do módulo aritmético n deum par de chaves RSA
dP	inteiro positivo satisfazendo e · dP = 1 (mod (p – 1)), expoente do sistema CRT correspondente ao fator primo p
dQ	inteiro positivo satisfazendo e · dQ = 1 (mod (q – 1)), expoente do sistema CRT correspondente ao fator primo q
e	inteiro positivo, expoente da chave pública RSA
EM	uma mensagem codificada em cadeia de octetos (Encoded Message)
emBits	comprimento (presumido) em bits de uma mensagem codificada EM
emLen	comprimento (presumido) em octetos de uma mensagem codificada EM
GCD (. , .)	máximo divisor comum de dois inteiros não negativos (e não simultaneamente nulos)
Hash	função de hash
hLen	comprimento em octetos da saída da função de hash Hash
k	comprimento em octetos do módulo aritmético n de um par de chaves RSA
L	cadeia de octetos para rótulo adicional do esquema de cifragem RSAES-OAEP
LCM (. ,..., .)	minimo múltiplo comum de uma lista de inteiros não negativos
m	inteiro entre 1 e n-1 que representa internamente uma mensagem
M	cadeia de octetos que forma uma mensagem
mask	cadeia de octetos produzida como saída da função MGF
maskLen	comprimento (presumido) em octetos de uma máscara mask
MGF	função geradora de máscaras mask
mgfSeed	cadeia de octetos de entrada (semente) para a função geradora de máscaras MGF
mLen	comprimento em octetos de uma mensagem M
n	módulo aritmético n  = r1 · r2 · … · ru , u > 2 de um par de chaves RSA
(n, e)	chave pública RSA
p, q	primeiros dois fatores primos de um módulo aritmético n ( p  = r1, q = r2 )
qInv	inteiro positivo que corresponde ao coeficiente CRT da equação q · qInv  = 1 (mod p)
ri	fator primo do módulo aritmético n de um par de chaves RSA, incluindo r1 = p, r2 = q
s	inteiro entre 0 e n-1 que representa internamente uma assinatura digital (autenticador)
S	assinatura digital representada como cadeia de octetos
sLen	comprimento em octetos do complemento salt de uma assinatura no esquema EMSA-PSS
ti	inteiros positivos correspondendo aos coeficientes dos fatores ri adicionais no sistema CRT onde r1 · r2 · … · ri-1 · ti  = 1 (mod ri) , i = 3, …, u
u	número de fatores primos (distintos) na decomposição do módulo aritmético n de um par de chaves RSA, u > 2
x	inteiro não negativo
X	cadeia de octetos correspondendo a x
xLen	comprimento (presumido) em octetos da cadeia de octetos X
0x	indicador de representação hexadecimal para um octeto ou cadeia de octetos;  “0x48” denota o octetp com valor hexadecimal 48;  “(0x)48 09 0e” denota a cadeia de três consecutivos octetos com valores hexadecimais 48, 09, e 0e, respectivamente.
phi(n)	LCM ( r1 – 1, r2 – 1, … , ru – 1)
||	operador de concatenação
XOR	função lógica "Ou exclusivo" bit a bit
CF( . )	Ceiling function, retorna o menor inteiro maior ou igual ao argumento (número real)

.
Chave Privada RSA (PKCS#1 v2.1)
.
A chave privada RSA tem dois formatos possíveis
.
a.1. o par (n, d), onde

n, inteiro positivo, é o módulo do par de chaves para a aritmética das primitivas do RSA
d inteiro positivo, é o expoente da chave privada para a aritmética das primitivas do RSA
.
a.2. a quíntupla (p, q, dP, dQ, qInv) e uma sequência (possivelmente vazia) de triplas  (r_i, d_i, t_i), i = 3,…, u,
onde
p   inteiro positivo, primeiro fator do módulo n
q    inteiro positivo, segundo fator do módulo n
dP   inteiro positivo, primeiro expoente no sistema de congruencias do resto chinês (CRT)
dQ   inteiro positivo, segundo expoente no sistema de congruencias do resto chinês (CRT)
qInv  inteiro positivo, primeiro coeficiente no sistema de congruencias do resto chinês (CRT)
r_i    inteiro positivo, i ésimo fator do módulo n
d_i   iinteiro positivo, i ésimo expoente no sistema de congruencias do resto chinês (CRT)
t_i   iinteiro positivo, i ésimo coeficiente no sistema de congruencias do resto chinês (CRT)
.
No caso da primeira representação (c.1), d é o inteiro positivo menor que n satisfazendo
 
 e · d = 1 (mod Phi(n))
.
onde e é o expoente da chave pública correspondente, Phi() é a função de Euler.
.
No caso da segunda representação (c.2),  p e q são os dois primeiros fatores do módulo aritmético do par de chaves  (i.e., r₁ and r₂), com os correspondentes expoentes do sistema CRT  dP e dQ satisfazendo
.
e · dP = 1 (mod (p – 1))
e · dQ = 1 (mod (q – 1))
.
e o coeficiente qInv do sistema CRT inteiro positivo menor que p satisfazendo
 
q · qInv  = 1 (mod p)
.
Se u > 2, a representação pode incluir uma ou mais triplass (r_i, d_i, t_i), i = 3, …, u. onde r_i são fatores primos adicionais do módulo aritmético n. Cara exponte d_i  (i = 3, …, u) do sistema CRT satisfiaz
.
e · d_i = 1 ( mod (r_i – 1) )
.
E cada coeficiente CRT  t_i (i = 3, …, u) é um inteiro positivo menor que ri satisfazendo
.
R_i · t_i = 1 (mod r_i)
onde R_i = r₁ · r₂ · ... · r_i–1.
.
.
C2-2.1.3 Primitivas de conversão de dados: I2OSP, OS2IP
.
a) I2OSP converte um inteiro não negativo numa cadeia de octetos.
.
I2OSP(x, xLen)
Entradas: x inteiro não negativo a ser convertido
xLen  comprimento pretendido para a cadeia de octetos convertida
Saída:   X cadeia de octetos coreespondente de comprimento xLen
Erro: “integer too large”
Algoritmo:

I2OSP(x,xLen)

1. If x > 256xLen , output “integer too large” and stop. 2. Write the integer x in its unique xLen-digit representation in base 256:  x = xxLen–1 256xLen-1 + xxLen–2 256xLen-2 + … + x1 256 + x0 , where 0 < xi < 256 (one or more leading digits will be zero if x is less than 256xLen–1 ). 3. Let the octet Xi have the integer value xxLen–i for 1 < i < xLen. Output the octet string X = X1 X2 … XxLen.

Fim do algoritmo
.
b) OS2IP converte uma cadeia de octetos em um número inteiro não negativo.
.
OS2IP(X)
Entrada: X cadeia de octetos a ser convertida
Saída: x  inteiro não negativo correspondente
Algoritmo:

OS2IP(X)

1. Let  X1 X2 … XxLen be the octets of X from first to last, and let xxLen–i be the integer value of the octet Xi for 1 < i < xLen 2. Let x = xxLen–1 256 xLen-1 + xxLen–2 256  xLen-2 + … + x1 256 + x0. 3. Output x.

Fim do algoritmo
 
.
C2-2.1.4 Primitivas criptográficas: RSAEP, RSADP, RSASP1, RSAVP1
.
a) RSAEP    primitiva de encriptação RSA
.
RSAEP((n, e), m)
Entradas: (n, e) chave pública RSA
m  inteiro entre 0 e n – 1 representante da mensagem a ser encriptada
Saída: c inteiro entre 0 e n – 1 representando o criptograma
Erro: “message representative out of range”
Premissa: chave pública RSA  (n, e) é válida
Algoritmo:

RSAEP((n,e),m)

1. If  m is not between 0 and n – 1, output “message representative out of range” and stop. 2. Let c = me mod n. 3. Output c.

Fim do algoritmo


b) RSADP  primitiva de decriptação RSA

RSADP (K, c)

Entradas: K chave privada RSA onde K tem uma dos seguintes formatos:
- o par (n, d)
- a quíntupla (p, q, dP, dQ, qInv) e uma sequência (possivelmente vazia) de triplas (r_i, d_i, t_i), i = 3,…, u,
c  inteiro entre 0 e n – 1 representando o criptograma
Saída: m  inteiro entre 0 e n – 1 representando a mensagem decifrada
Erro: “ciphertext representative out of range”
Premissa: a chave privada RSA K é válida e identifica o portador.
Algoritmo:

RSADP(K,c)

1. If  c is not between 0 and n – 1, output “ciphertext representative out of range” and stop. 2. The message representative m is computed as follows. a. If the first form (n, d) of K is used, let m = cd mod n. b. If the second form (p, q, dP, dQ, qInv) and (ri, di, ti) of K is used, proceed as follows:  i. Let m1 = cdP mod p and m2 = cdQ mod q.  ii. If u > 2, let mi = cdi mod ri, i = 3, …, u.  iii. Let h = (m1 – m2) · qInv mod p.  iv. Let m = m2 + q · h. v. If u > 2, let R = r1 and for i = 3 to u do 1. Let R = R · ri–1. 2. Let h = (mi – m) · ti (mod ri). 3. Let m = m + R · h. 3. Output m.

Fim do algoritmo
.
Nota. Passo 2 pode ser reescrito como um único laço, desde que se reverta a ordem de p e q. Todavia, para se ter consistência com a versão v2.0 do PKCS#1, os dois primos p e q são tratados separadamente dos demais primos fatores de n.
.
c) RSASP1 Primitva para lavra de assinatura digital (autenticador)
.
RSASP1 (K, m)
Entradas: chave privada RSA K onde K tem uma dos seguintes formatos:
- o par (n, d)
- a quíntupla (p, q, dP, dQ, qInv) e uma sequência (possivelmente vazia) de triplas (r_i, d_i, t_i), i = 3,…, u,
m  inteiro entre 0 e n – 1 representando a mensagem a ser assinada
Saída: s  inteiro entre 0 e n – 1 representando a lavra da assinatura na mensagem m pela chave K
Erro: “ciphertext representative out of range”
Algoritmo:

RSASP1(K,m)

1. If  m is not between 0 and n – 1, output “message representative out of range” and stop. 2. The signature representative s is computed as follows.  a. If the first form (n, d) of K is used, let s = md mod n.  b. If the second form (p, q, dP, dQ, qInv) and  (ri, di, ti) of K is used, proceed as follows:   i. Let s1 = mdP mod p and s2 = mdQ mod q. ii. If u > 2, let si = mdi mod ri, i = 3, …, u. iii. Let h = (s1 – s2) · qInv mod p. iv. Let s = s2 + q · h. v. If u > 2, let R = r1 and for i = 3 to u do 1. Let R = R · ri–1. 2. Let h = (si – s) · ti (mod ri). 3. Let s = s + R · h. 3. Output s.

Fim do algoritmo
.
d) RSAVP1 Primitva para verificação de assinatura digital (autenticador)

RSAVP1 ((n, e), s)

Entradas: (n, e) chave pública RSA
s  inteiro entre 0 e n – 1 representando a assinatura RSA sobre uma mensagem
Saída: m inteiro entre 0 e n – 1 representando a mensagem cuja integridade e origem se pretende verificar
Erro: “signature representative out of range”
Algoritmo:

RSAVP1((n,e),s)

1. If s is not between 0 and n – 1, output “signature representative out of range” and stop. 2. Let m = se mod n. 3. Output m.

Fim do algoritmo

AULA 4

C2-2.1.5 Esquemas (protocolos) de cifragem: RSAES-OAEP e RSAES-PKCSI v1_5

Para uma justificativa referente ao projeto e características de segurança desses esquemas, sustentada em análise de risco baseada na literatura científica conhecida a respeito, que procura mensurar o custo computacional das formas de ataque conhecidas aos respectivos mecanismos de assinatura e cifragem, verificar em [4] seção 7 (pags 14 a 17)

a) RSAES-OAEP (Rogaway's “Optimal Asymmetric Encryption Padding.”)

RSAES-OAEP-ENCRYPT ((n, e), M, L)

Opções: Hash função de hash (hLen denota o comprimento em octetos da saída da função de hash)
MGF função geradora de máscaras.
Entrada: (n, e) chave pública RSA do destinatário (k denota o comprimento em octeto do módulo n)
M messagem a ser encriptada, uma cadeia de octetos de comprimento mLen < k – 2·hLen – 2
L rótulo opcional associado à messagem; cujo valor default, se L não é fornecido, é a cadeia vazia
Saída: C cadeia de octetos do criptograma de comprimento k
Erros: “message too long”; “label too long”
Premissa: chave pública RSA (n, e) é válida, e seu transporte identifica o destinatário
Algoritmo:

RSAES-OAEP-ENCRYPT((n,e),M,L)

1. Length checking: a. If the length of L is greater than the input limitation for the hash function (261 – 1 octets for SHA-1), output “label too long” and stop. b. If mLen > k – 2·hLen – 2, output “message too long” and stop. 2. EME-OAEP encoding (see Figure 1 below): a. If the label L is not provided, let L be the empty string. Let lHash = Hash (L), an octet string of length hLen (see the note below). b. Generate an octet string PS consisting of k – mLen – 2·hLen – 2 zero octets. The length of PS may be zero. c. Concatenate lHash, PS, a single octet with hexadecimal value 0x01, and the message M to form a data block DB of length k – hLen – 1 octets as DB = lHash || PS || 0x01 || M . d. Generate a random octet string seed of length hLen. e. Let dbMask = MGF(seed, k – hLen – 1) f. Let maskedDB = DB XOR dbMask. g. Let seedMask = MGF(maskedDB, hLen). h. Let maskedSeed = seed XOR seedMask. i. Concatenate a single octet with hexadecimal value 0x00, maskedSeed, and maskedDB to form an encoded message EM of length k octets as EM = 0x00 || maskedSeed || maskedDB. 3. RSA encryption: a. Convert the encoded message EM to an integer message representative m (2.1.3, ref [4] Section 4.2); m = OS2IP (EM) . b. Apply the RSAEP encryption primitive (Section 5.1.1) to the RSA public key (n, e) and the message representative m to produce an integer ciphertext representative c: c = RSAEP ((n, e), m) . c. Convert the ciphertext representative c to a ciphertext C of length k octets (2.1.3, ref [4] Section 4.1); C = I2OSP(c, k) . 4. Output the ciphertext C.

Fim do algoritmo
Diagrama do acolchoamento (padding) OAEP:

.
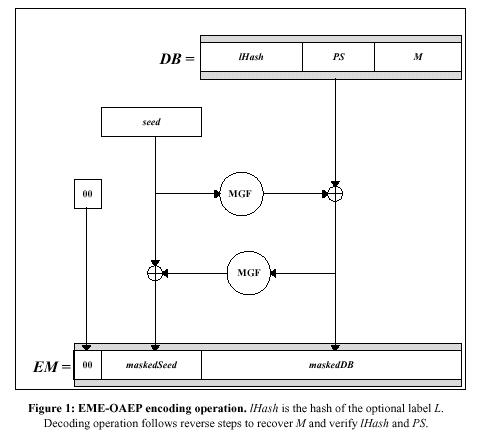
RSAES-OAEP-DECRYPT (K, C, L)
Opções: Hash função de hash (hLen denota o comprimento em octetos da saída da função de hash)
MGF função geradora de máscaras.
Entrada: chave privada RSA K do destinatário-receptor (k denota o comprimento em octeto do módulo n);
C cadeia de octetos do criptograma a ser dencriptado, de comprimento k > 2·hLen + 2;
L rótulo opcional associado à messagem; cujo valor default, se L não é fornecido, é a cadeia vazia.
Saída: M messagem de comprimento mLen < k – 2·hLen – 2.
Erros: “decryption error”.
Premissa: chave privada RSA K é válida, e identifica o destinatário-receptor.
Algoritmo:

RSAES-OAEP-DECRYPT(K,C,L)

1. Length checking: a. If the length of L is greater than the input limitation for the hash function (261 – 1 octets for SHA-1), output “decryption error” and stop. b. If the length of the ciphertext C is not k octets, output “decryption error” and stop. c. If k < 2hLen + 2, output “decryption error” and stop. 2. RSA decryption: a. Convert the ciphertext C to an integer ciphertext representative c (2.1.3, ref [4] Section 4.2): c = OS2IP(C) . b. Apply the RSADP decryption primitive (2.1.4, ref [4] Section 5.1.2) to the RSA private key K and the ciphertext representative c to produce an integer message representative m:  m = RSADP(K, c) If RSADP outputs “ciphertext representative out of range” (meaning that c > n), output “decryption error” and stop. c. Convert the message representative m to an encoded message EM of length k octets (2.1.3, ref [4] Section 4.2): EM = I2OSP(m, k) . 3. EME-OAEP decoding: a. If the label L is not provided, let L be the empty string. Let lHash = Hash(L), an octet string of length hLen (see the note in figure.1). b. Separate the encoded message EM into a single octet Y, an octet string maskedSeed of length hLen, and an octet string maskedDB of length k - hLen - 1 as EM = Y || maskedSeed || maskedDB. c. Let seedMask = MGF(maskedDB, hLen). d. Let seed = maskedSeed XOR seedMask. e. Let dbMask = MGF(seed, k – hLen – 1). f. Let DB = maskedDB XOR dbMask. g. Separate DB into an octet string lHash’ of length hLen, a (possibly empty) padding string PS consisting of octets with hexadecimal value 0x00, and a message M as DB = lHash’ || PS || 0x01 || M . If there is no octet with hexadecimal value 0x01 to separate PS from M, if lHash does not equal lHash’, or if Y is nonzero, output “decryption error” and stop. (See the note below.) 4. Output the message M..

Fim do algoritmo

Nota: ref [4] pag 21 explica porque as mensagens de erro dos diferentes passos do esquema acima devem ser indistinguiveis.

 
b) RSAES-PKCSIv1_5
 
A implementação do padrão de encriptação (RSAES) na versão PKCSv1.5 requer algumas medidas cautelares, em função do avanço das técnicas de ataque ao RSA conhecidas da literatura de criptoanálise dos protocolos SSL e TLS (que empregam o padrão PKCSv1.5). Essas medidas são citadas em ref [4] pag 22.


RSAES-PKCSIv1_5-ENCRYPT ((n, e), M)

Entrada:(n, e)  chave pública RSA do destinatário (k denota o comprimento em octeto do módulo n)
M messagem a ser encriptada, uma cadeia de octetos de comprimento mLen < k – 11
Saída: C cadeia de octetos do criptograma de comprimento k
Erros: “message too long”;
Premissa: chave pública RSA (n, e) é válida, e seu transporte identifica o destinatário
Algoritmo:

RSAES-PKCSIv1_5-ENCRYPT((n,e),M)

1. Length checking: If mLen > k – 11, output “message too long” and stop. 2. EME-PKCS1-v1_5 encoding: a. Generate an octet string PS of length k – mLen – 3 consisting of pseudo-randomly generated nonzero octets. The length of PS will be at least eight octets. b. Concatenate PS, the message M, and other padding to form an encoded message EM of length k octets as EM = 0x00 || 0x02 || PS || 0x00 || M . 3. RSA encryption: a. Convert the encoded message EM to an integer message representative m (2.1.3 ref [4] Section 4.2): m = OS2IP(EM) . b. Apply the RSAEP encryption primitive (Section 5.1.1) to the RSA public key (n, e) and the message representative m to produce an integer ciphertext representative c: c = RSAEP((n, e), m) . c. Convert the ciphertext representative c to a ciphertext C of length k octets: C = I2OSP(c, k) . 4. Output the ciphertext C.

Fim do algoritmo
.
RSAES-PKCS1-V1_5-DECRYPT (K, C)
Entrada: K chave privada RSA do destinatário-receptor
C cadeia de octetos do criptograma a ser dencriptado, de comprimento k = comprimento em octeto do módulo n
Saída: M messagem de comprimento mLen < k – 11
Erros: “decryption error”
Premissa: chave privada RSA K é válida, e identifica o destinatário-receptor
Algoritmo:

RSAES-PKCS1-V1_5-DECRYPT(K,C)

1. Length checking: If the length of C is not k octets (or if k < 11), output “decryption error” and stop. 2. RSA decryption: a. Convert the ciphertext C to an integer ciphertext representative c (see ref. [4] Section 4.2): c = OS2IP(C) . b. Apply the RSADP decryption primitive (2.1.4 ref. [4] Section 5.1.2) to the RSA private key (n, d) and the ciphertext representative c to produce an integer message representative m: m = RSADP((n, d), c) . If RSADP outputs “ciphertext representative out of range” (meaning that c > n), output “decryption error” and stop. c. Convert the message representative m to an encoded message EM of length k octets: EM = I2OSP(m, k) . 3. EME-PKCS1-v1_5 decoding: Separate the encoded message EM into an octet string PS consisting of nonzero octets and a message M as EM = 0x00 || 0x02 || PS || 0x00 || M .  If the first octet of EM does not have hexadecimal value 0x00, if the second octet of EM does not have hexadecimal value 0x02, if there is no octet with hexadecimal value 0x00 to separate PS from M, or if the length of PS is less than 8 octets, output “decryption error” and stop. (See the note below.) 4. Output M.

Fim do algoritmo

Nota: ref [4] pag 21 explica porque as mensagens de erro dos diferentes passos do esquema acima devem ser indistinguiveis.
 

C2-2.1.6 Esquemas (protocolos) de assinatura: RSASSA-PSS e RSASSA-PKCSI v1_5
 
Esquemas de assintura digital constituem-se de um par de protocolos complementares. Um para lavra e outro para verificação de assinaturas digitais. Um protocolo para verificação de assinaturas, por sua vez, usa operação criptográfica para um dentre dois possíveis objetivos imediatos. Ou para recuperarção da mensagem autenticada (scheme by message recovery), ou para validação do autenticador apensado à representação de uma mensagem autenticada ( scheme with signature appendix). O padrão PKCS#1 versão 2.1 estabelece dois esquemas de assinatura digital, PSS e PKCSIv1_5, ambos usando o método do autenticador apensado.

Um dos motivos para a escolha desse método, baseado no padrão IEEE 1363-2000, é a possibilidade dos esquemas de assinatura digital nele modelados se integrarem a protocolos mais complexos que procuram suprir as premissas do conceito de assinatura digital de forma escalável em redes abertas, como em PKIs baseadas no padrão X.509. Este método, porém, apresenta características de segurança (vistas no curso C.1) que indicam a sua atomização (single pass). Em situações onde o cálculo do hash da mensagem precisa ser separado do processo critpográfico sobre os autenticadores apensáveis, deve-se buscar outro padrão para o esquema de assinatura, como o atual PKCS#7.
 

a) RSASSA-PSS: Esquema de assinatura digital v2.1
 
A implementação do padrão de esquema de assinatura (RSASSA) na versão PSS combina as primitivas RSASP1 e RSAVP1 com o método de codificação EMSA-PSS, que é compatível com o esquema definido pelo padrão IFSSA em IEEE 1363-2000, atualizada na proposta de draft IEEE P1363, onde o método de codificação PSS é descrito pelo padrão EMSA4. EMSA4 é um pouco mais genérico que o PSS, por descrever a codificação de mensagens representada por cadeias de bits, enquando o PSS se restringe a cadeia de octetos, usando a mesma codificação.

O esquema RSASSA-PSS opera com mensagens autenticáveis de comprimento irrestrito ou restrito por um número muito grande, dependendo da função de hash implementada pela codificação EMSA-PSS. O método de codificação EMSA-PSS é recomendado como alternativa ao método usado no padrão PKCS#1v1.5, contra possíveis desenvolvimentos futuros da criptoanálise de chaves públicas. Para uma justificativa, são citadas referencias e estudos em ref [4] pag 30.
 

RSASSA-PSS-SIGN (K, M)
Entrada: K chave privada RSAdo remetente-autenticador
M cadeia de octetos da mensagem a ser digitalmente assinada
Saída: S autenticador (assinatura) do titular de K sobre a messagem M de comprimento k, onde k = comprimento em octeto do módulo n
Erros:  “message too long”; “RSA modulus too short”
Premissa: chave privada RSA K é válida, e identifica o remetente-autenticador
Algoritmo:

RSAES-PSS-SIGN(K,M)

1. EMSA-PSS encoding: Apply the EMSA-PSS encoding operation ( ref [4] Section 9.1.1) to the message M to produce an encoded message EM of length CF( (modBits – 1)/8 ) octets such that the bit length of the integer OS2IP(EM) (see ref [4] Section 4.2) is at most modBits – 1, where modBits is the length in bits of the RSA modulus n: EM = EMSA-PSS-ENCODE(M, modBits – 1) . Note that the octet length of EM will be one less than k if modBits – 1 is divisible by 8 and equal to k otherwise. If the encoding operation outputs “message too long,” output “message too long” and stop. If the encoding operation outputs “encoding error,” output “encoding error” and stop. 2. RSA signature: a. Convert the encoded message EM to an integer message representative m (2.1.3 ref [4] Section 4.2): m = OS2IP(EM) . b. Apply the RSASP1 signature primitive ( ref [4] Section 5.2.1) to the RSA private key K and the message representative m to produce an integer signature representative s: s = RSASP1(K,m). c. Convert the signature representative s to a signature S of length k octets (2.1.3 ref [4] Section 4.1): S = I2OSP(s, k) . 3. Output the signature S.

Fim do algoritmo
.
RSASSA-PSS-VERIFY ((n, e), M, S)
Entrada: chave pública RSA (n, e) do signatário
M cadeia de octetos representando a messagem cuja assinatura apensada se pretende verificar
S cadeia de octetos de comprimento k representando o autenticador (assinatura apensada) à mensagem M, onde k é o comprimento em octetos do módulo aritmético da chave pública (n,e)
Saída: “valid signature” ou “invalid signature”
Erros: “message too long”; “RSA modulus too short”
Algoritmo:

RSAES-PSS-VERIFY((n,e),M,S)

1. Length checking: If the length of the signature S is not k octets, output “invalid signature” and stop. 2. RSA verification: a. Convert the signature S to an integer signature representative s (2.1.3 ref [4] Section 4.2): s = OS2IP(S) . b. Apply the RSAVP1 verification primitive ( ref [4] Section 5.2.2) to the RSA public key (n, e) and the signature representative s to produce an integer message representative m: m = RSAVP1((n, e), s) . If RSAVP1 output “signature representative out of range,” output “invalid signature” and stop. c. Convert the message representative m to an encoded message EM of length emLen = é(modBits – 1)/8ù octets, where modBits is the length in bits of the RSA modulus n (see ref [4]  Section 4.1): EM = I2OSP(m, emLen) . Note that emLen will be one less than k if modBits – 1 is divisible by 8 and equal to k otherwise. If I2OSP outputs “integer too large,” output “invalid signature” and stop. 3. EMSA-PSS verification: Apply the EMSA-PSS verification operation ( ref [4] Section 9.1.2) to the message M and the encoded message EM to determine whether they are consistent: Result = EMSA-PSS-VERIFY(M, EM, modBits – 1) . 4. If Result = “consistent,” output “valid signature.” Otherwise, output “invalid signature.”

Fim do algoritmo
.
b) RSASSA-PKCS1-V1_5: Esquema de assinatura digital v1.5
 
A implementação do padrão de esquema de assinatura (RSASSA) na versão PKCSv1.5 combina as primitivas RSASP1 e RSAVP1 com o método de codificação EMSA-PKCS1-v1_5, que é compatível com o esquema definido pelo padrão IFSSA em IEEE 1363-2000 ( EMSA usado no PKCS1-v1_5 não está definida em IEEE 1363-2000, mas é proposta no draft IEEE P1363).

O esquema RSASSA-PKCS1-v1_5 opera com mensagens autenticáveis de comprimento irrestrito ou restrito por um número muito grande, dependendo da função de hash implementada pela codificação EMSA. Enquanto nenhum ataque é conhecido na literatura científica contra o método de codificação EMSA-PKCS-v1_5, uma transição gradual para o método EMSA-PSS é recomendada como precaução, contra os possíveis desenvolvimentos futuros da criptoanálise de chaves públicas. Para uma justificativa, são citadas referencias e estudos em ref [4] pag 30.
 

RSASSA-PKCS1-V1_5-SIGN (K, M)
Entrada: chave privada RSA K do remetente-autenticador
M cadeia de octetos da mensagem a ser digitalmente assinada
Saída: S autenticador (assinatura) do titular de K sobre a messagem M de comprimento k, onde k = comprimento em octeto do módulo n
Erros:  “message too long”; “RSA modulus too short”
Premissa: chave privada RSA K é válida, e identifica o remetente-autenticador
Algoritmo:

RSAES-PKCS1-V1_5-SIGN(K,M)

1. EMSA-PKCS1-v1_5 encoding:  Apply the EMSA-PKCS1-v1_5 encoding operation (see ref. [4] Section 9.2) to the message M to produce an encoded message EM of length k octets: EM = EMSA-PKCS1-V1_5-ENCODE(M, k) . If the encoding operation outputs “message too long,” output “message too long” and stop. If the encoding operation outputs “intended encoded message length too short,” output “RSA modulus too short” and stop. 2. RSA signature: a. Convert the encoded message EM to an integer message representative m (2.1.3 ref. [4] Section 4.2): m = OS2IP (EM) . b. Apply the RSASP1 signature primitive (see ref. [4] Section 5.2.1) to the RSA private key K and the message representative m to produce an integer signature representative s: s = RSASP1 (K, m) . c. Convert the signature representative s to a signature S of length k octets (2.1.3 ref. [4]  Section 4.1): S = I2OSP (s, k) 3. Output the signature S.

Fim do algoritmo
.
RSASSA-PKCS1-V1_5-VERIFY ((n, e), M, S)
Entrada: chave pública RSA (n, e) do signatário
M cadeia de octetos representando a messagem cuja assinatura apensada se pretende verificar
S cadeia de octetos de comprimento k representando o autenticador (assinatura apensada) à mensagem M, onde k é o comprimento em octetos do módulo aritmético da chave pública (n,e)
Saída: “valid signature” ou “invalid signature”
Erros: “message too long”; “RSA modulus too short”
Algoritmo:

RSAES-PKCSIv1_5-VERIFY((n,e),M,S)

1. Length checking:  If the length of the signature S is not k octets, output “invalid signature” and stop. 2. RSA verification: a. Convert the signature S to an integer signature representative s (2.1.3 ref.[4] Section 4.2): s = OS2IP (S) . b. Apply the RSAVP1 verification primitive (2.1.4 ref.[4] Section 5.2.2) to the RSA public key (n, e) and the signature representative s to produce an integer message representative m: m = RSAVP1 ((n, e), s).  If RSAVP1 outputs “signature representative out of range,” output “invalid signature” and stop. c. Convert the message representative m to an encoded message EM of length k octets (see Section 4.1): EM’ = I2OSP (m, k) . If I2OSP outputs “integer too large,” output “invalid signature” and stop. 3. EMSA-PKCS1-v1_5 encoding: Apply the EMSA-PKCS1-v1_5 encoding operation (Section 9.2) to the message M to produce a second encoded message EM’ of length k octets: EM’ = EMSA-PKCS1-V1_5-ENCODE(M, k) . If the encoding operation outputs “message too long,” output “message too long” and stop. If the encoding operation outputs “intended encoded message length too short,” output “RSA modulus too short” and stop. 4. Compare the encoded message EM and the second encoded message EM’. If they are the same, output “valid signature”; otherwise, output “invalid signature.”..

Fim do algoritmo
.
c) EMSA: Métodos de codificação para esquemas de assinatura digital

c.1 EMSA-PSS
 

Esse método de codificação é parametrizado pela escolha de função de hash, função geradora de máscaras e comprimento de valor salt. Esses parâmetros podem ser fixados para um par de chaves RSA, exeto para o valor de salt, que pode variar. (ref. [4] discute detalhes na pag. 33, e também sugestões de escolhas default para os parâmetros, no apêndice B). Este método, cujo esquema é mostrado na figura 2 abaixo, é baseado no Probabilistic Signature Scheme de Bellare e Rogaway (ver [4])

EMSA-PSS-ENCODE (M, emBits)
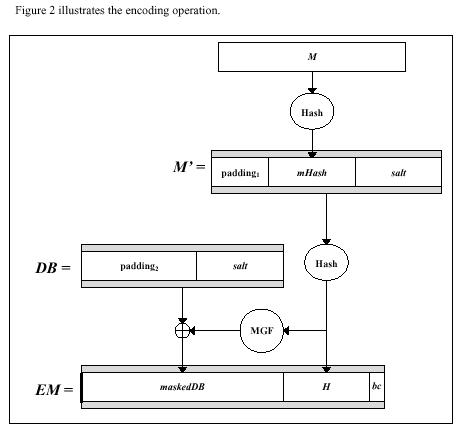
Opções: Hash função de hash (hLen denota o comprimento em octetos da saída da função de hash)
MGF função geradora de máscaras.
sLen comprimento pretendido para o valor de salt.
Entrada: M messagem a ser codificada, cadeia de octetos de comprimento mLen < k – 2·hLen – 2.
emBits tamanho máximo em bits do inteiro OS2IP(EM) (ver ref. [4] Section 4.2), pelo menos  8hLen + 8sLen + 9
Saída:  EM mesagem codificada, cadeia de octetos de comprimento emLen = CF(emBits/8);
Erros: “encoding error”, “message too long”.
Algoritmo:

EMSA-PSS-ENCODE(M,emBits)

1. If the length of M is greater than the input limitation for the hash function (261 – 1 octets for SHA-1), output “message too long” and stop. 2. Let mHash = Hash (M), an octet string of length hLen. 3. If emLen < hLen + sLen + 2, output “encoding error” and stop. 4. Generate a random octet string salt of length sLen; if sLen = 0, then salt is the empty string. 5. Let M’ = (0x)00 00 00 00 00 00 00 00 || mHash || salt; M’ is an octet string of length 8 + hLen + sLen with eight initial zero octets. 6. Let H = Hash (M’), an octet string of length hLen. 7. Generate an octet string PS consisting of emLen – sLen – hLen – 2 zero octets. The length of PS may be 0. 8. Let DB = PS || 0x01 || salt; DB is an octet string of length emLen – hLen – 1. 9. Let dbMask = MGF (H, emLen – hLen – 1). 10. Let maskedDB = DB XOR dbMask. 11. Set the leftmost 8 emLen – emBits bits of the leftmost octet in maskedDB to zero. 12. Let EM = maskedDB || H || (0x)bc. 13. Output EM.

Fim do algoritmo.
.
EMSA-PSS-VERIFY (M, EM, emBits)
Opções: Hash função de hash (hLen denota o comprimento em octetos da saída da função de hash)
MGF função geradora de máscaras.
sLen comprimento pretendido para o valor de salt.
Entrada: M messagem a ser codificada, cadeia de octetos de comprimento mLen < k – 2·hLen – 2.
EM mesagem codificada, cadeia de octetos de comprimento emLen = CF(emBits/8);
emBits tamanho máximo em bits do inteiro OS2IP(EM) (ver ref. [4] Section 4.2), pelo menos  8hLen + 8sLen + 9
Saída: “consistent”, “inconsistent”.
Algoritmo:

EMSA-PSS-VERIFY(M,EM,emBits)

1. If the length of M is greater than the input limitation for the hash function (261 – 1octets for SHA-1), output “inconsistent” and stop. 2. Let mHash = Hash (M), an octet string of length hLen. 3. If emLen < hLen + sLen + 2, output “inconsistent” and stop. 4. If the rightmost octet of EM does not have hexadecimal value 0xbc, output “inconsistent” and stop. 5. Let maskedDB be the leftmost emLen – hLen – 1 octets of EM, and let H be the next hLen octets. 6. If the leftmost 8emLen – emBits bits of the leftmost octet in maskedDB are not all equal to zero, output “inconsistent” and stop. 7. Let dbMask = MGF (H, emLen – hLen – 1). 8. Let DB = maskedDB XOR dbMask. 9. Set the leftmost 8emLen – emBits bits of the leftmost octet in DB to zero. 10. If the emLen – hLen – sLen – 2 leftmost octets of DB are not zero or if the octet at position emLen – hLen – sLen – 1 (the leftmost position is “position 1”) does not have hexadecimal value 0x01, output “inconsistent” and stop. 11. Let salt be the last sLen octets of DB. 12. Let M’ = (0x)00 00 00 00 00 00 00 00 || mHash || salt ; M’ is an octet string of length 8 + hLen + sLen with eight initial zero octets. 13. Let H’ = Hash (M’), an octet string of length hLen. 14. If H = H’, output “consistent.” Otherwise, output “inconsistent.”

Fim do algoritmo
.
c.2 EMSA-PKCS1-v1_5
 
Esse método de codificação é determinístico e contempla apenas o processo de codificação
.
EMSA-PKCS1-v1_5-ENCODE (M, emLen)
Opções: Hash função de hash (hLen denota o comprimento em octetos da saída da função de hash)
Entrada: M messagem a ser codificada, cadeia de octetos
emLen tamanho em octetos pretendido da mensagem codificada > tLen + 11, onde tLen é o comprimento em octetos da codificação T de um certo valor computado durante a operação de codificação.
Saída: EM mesagem codificada, cadeia de octetos de comprimento emLen
Erros: “message too long”, “intended encoded message lenght too short”.
Algoritmo:

EMSA-PKCS1-v1_5-ENCODE(M,emLen)

1. Apply the hash function to the message M to produce a hash value H: H = Hash (M) . If the hash function outputs “message too long,” output “message too long” and stop. 2. Encode the algorithm ID for the hash function and the hash value into an ASN.1 value of type DigestInfo (see Appendix A.2.4) with the Distinguished Encoding Rules (DER), where the type DigestInfo has the syntax DigestInfo ::= SEQUENCE  {     digestAlgorithm AlgorithmIdentifier,     digest OCTET STRING } The first field identifies the hash function and the second contains the hash value. Let T be the DER encoding of the DigestInfo value (see the notes below) and let tLen be the length in octets of T. 3. If emLen < tLen + 11, output “intended encoded message length too short” and stop. 4. Generate an octet string PS consisting of emLen – tLen – 3 octets with hexadecimal value 0xff. The length of PS will be at least 8 octets. 5. Concatenate PS, the DER encoding T, and other padding to form the encoded message EM as EM = 0x00 || 0x01 || PS || 0x00 || T . 6. Output EM.

Notes. 1. For the six hash functions mentioned in Appendix B.1, the DER encoding T of the DigestInfo value is equal to the following: MD2: (0x)30 20 30 0c 06 08 2a 86 48 86 f7 0d 02 02 05 00 04 10 || H. MD5: (0x)30 20 30 0c 06 08 2a 86 48 86 f7 0d 02 05 05 00 04 10 || H. SHA-1: (0x)30 21 30 09 06 05 2b 0e 03 02 1a 05 00 04 14 || H. SHA-256: (0x)30 31 30 0d 06 09 60 86 48 01 65 03 04 02 01 05 00 04 20 || H. SHA-384: (0x)30 41 30 0d 06 09 60 86 48 01 65 03 04 02 02 05 00 04 30 || H. SHA-512: (0x)30 51 30 0d 06 09 60 86 48 01 65 03 04 02 03 05 00 04 40 || H. 2. In version 1.5 of this document, T was defined as the BER encoding, rather than the DER encoding, of the DigestInfo value. In particular, it is possible – at least in theory – that the verification operation defined in this document (as well as in version 2.0) rejects a signature that is valid with respect to the specification given in PKCS #1 v1.5. This occurs if other rules than DER are applied to DigestInfo (e.g., an indefinite length encoding of the underlying SEQUENCE type). While this is unlikely to be a concern in practice, a cautious implementer may choose to employ a verification operation based on a BER decoding operation as specified in PKCS #1 v1.5. In this manner, compatibility with any valid implementation based on PKCS #1 v1.5 is obtained. Such a verification operation should indicate whether the underlying BER encoding is a DER encoding and hence whether the signature is valid with respect to the specification given in this document.

Fim do algoritmo

O apêndice A da ref [4] descreve, entre as páginas 39 a 46, os tipos ASN-1 de todas as estruturas de dados utilizadas nos algoritmos aqui descritos

Esse padrão, cuja versão aqui resumida teve sua última revisão em novembro de 1993 [5], descreve a sintaxe para representação de chaves privadas do algoritmo RSA e informações pertinentes. Essas informações incluem aquelas relativas ao processo de cifragem para armazenamento (processo descrito no padrão PKCS#5) e um conjunto de atributos representando as premissas de confiança para o uso da chave, incluindo nome do titular e nome distinguido da entidade certificadora do par público da chave privada.

Uma lista não exaustiva desses atributos pode ser encontrada no documento que descreve o padrão PKCS#9
 

A definição do tipo ASN.1 para informação sobre chaves privadas deve ser
 

type PrivateKeyInfo

PrivateKeyInfo ::= SEQUENCE  {     version Version,     privateKeyAlgorithm PrivateKeyAlgorithmIdentifier,     privateKey PrivateKey,     attributes [0] IMPLICIT Attributes OPTIONAL  } Version ::= INTEGER PrivateKeyAlgorithmIdentifier ::= AlgorithmIdentifier PrivateKey ::= OCTET STRING Attributes ::= SET OF Attribute

A semântica dos campos desse tipo corresponde a:

• version é o número de versão da sintaxe, para compatibilidade com versões futuras deste padrão. Deve ser 0 para esta versão deste padrão.
• privateKeyAlgorithm identifica o algoritmo para o qual foi gerada a chave privada, conforme descritos no padrão PKCS #1. Um exemplo de valor para este campo seria rsaEncryption.
• privateKey é a cadeia de octetos cujo conteúdo constitui os valores da chave privada. A interpretação desse conteúdo é definida no registro do algoritmo. Para uma dada chave privada RSA, corresponde ao valor codificado segundo as regras BER para o tipo RSAPrivateKey, descritos no apêndice A do padrão PKCS#1 (ref [4]).
• attributes Conjunto de valores que informam sobre o uso pretendido para tal chave privada, encriptados junto com a respectiva chave privada.

   C2-2.2.2 Sintaxe de informação sobre chaves privadas encriptadas

A definição do tipo ASN.1 para informação sobre chaves privadas encriptadas deve ser
 

type EncryptedPrivateKeyInfo

EncryptedPrivateKeyInfo ::= SEQUENCE  {     encryptionAlgorithm EncryptionAlgorithmIdentifier,     encryptedData EncryptedData  } EncryptionAlgorithmIdentifier ::= AlgorithmIdentifier EncryptedData ::= OCTET STRING

A semântica dos campos desse tipo corresponde a:

• encryptionAlgorithm identifica o algoritmo sob o qual a informação sobre uma chave privada foi encriptada. Dois exemplos, descritos no documento que estabelece o padrão PKCS#5 são  pbeWithMD2AndDES-CBC e pbeWithMD5AndDES-CBC.p
• encryptedData é a informação sobre uma chave privada devidamente encriptada

O processo de encriptação envolve dois passos:

1. 1. A informação sobre uma chave privada é codificada segundo as regras BER, resultando numa cadeia de octetos.
2. 2. A cadeia de octetos resultante do passo 1 é encriptada com uma chave secreta (normalmente derivada de uma "senha de acesso")

Bibliografia

Material de referência

Texto de Referência

· Housley, R. & Polk, T.: "Planning for PKI" ,
 John Willey & Sons, 2001, New York

· Rezende, P.: "Curso C2 - ICP"  (módulos 1 a 6),

Material de consulta

Os textos abaixo aprofundam o material abordado no curso.

• [1] Autor anônimo?,  "ASN-1, DER e BER", Univ. Federal do Rio de Janeiro - .pdf - 37 pag
• [2] Curso pós em Redes de computadores - UFRGS:  "O uso de ASN.1 para especificação formal de protocolos", Univ. Federal do Rio Grande do Sul - .pdf - 16 pag
• [3] ITU-T X.208 "ASN-1 Specification", Melbourne, 1988 - pdf - 74 pag.

      ITU-T X.209 "BER for ASN-1 Specification", Melbourne, 1988, 1993 - pdf - 26 pag.
(Obs: A especificação ASN.1 do tipo OBJECT IDENTIFIER está no documento do padrão ITU X.680)
• [4] “RSA Security Inc. Public-Key Cryptography Standards (PKCS)”: PKCS#1 v2.1
• [5] “RSA Security Inc. Public-Key Cryptography Standards (PKCS)”: PKCS#8